こんにちは！Eukaryaの矢所です。

現在Eukaryaでは、GoogleのDracoライブラリをRustプログラミング言語で書き直した、draco-oxideを開発しています。最近、アルファバージョンをcrates.ioでリリースしました。まだ開発途中ですが、気になる方はぜひチェックしてみてください。

https://github.com/reearth/draco-oxide

本稿では、3Dグラフィックスにおけるメッシュ圧縮技術に関する連載の第一回目として、Edgebreakerアルゴリズムについて解説していきます。

メッシュとは

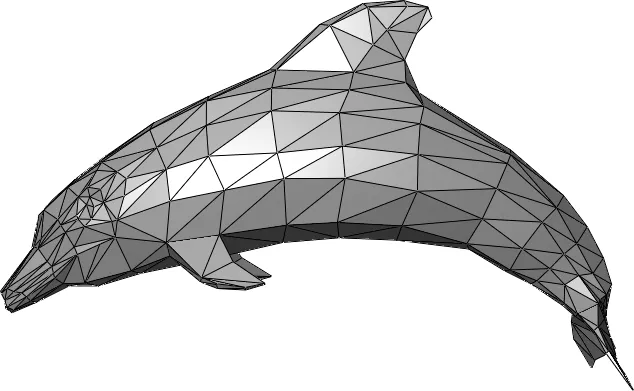
メッシュとは、3Dモデルにおける点群とその点群を頂点とする三角形の集合のことを指します。メッシュは3Dグラフィックスにおいて基本的なデータ構造であり、様々な曲面を画面上に表示するために使用されます。

Edgebreakerとは

本稿では、メッシュの内の三角形の集合の部分を「メッシュの接続性」と呼ぶことにします。

今回の記事で解説していくEdgebreakerアルゴリズムは、このメッシュの接続性を圧縮するためのものです。

Edgebreakerは、他の圧縮技術と組み合わせることで、最良の場合、メッシュの接続性データを元のサイズの1%未満にまで圧縮することができる、とても強力なアルゴリスムです。この高い圧縮率と簡潔さから、メッシュ接続性圧縮の標準アルゴリズムの一つとして知られており、GoogleのDracoライブラリなどの主要なメッシュ圧縮ライブラリで採用されています。

Edgebreakerアルゴリズムは、円盤または球面に同相のメッシュ表面に対してRossignac（1999）によって最初に導入され、その後、複数の境界を持つ他の向き付け可能な二次多様体にまで拡張されました。

アルゴリズムの基本的なアイデアは非常に簡潔です。

隣接する三角形をたどりながら再帰的に各三角形を見ていき、接続性に関する局所的な情報を調べます。そしてこれらの情報を事前に定められた記号の1つとして記録することで、接続性データを記号の文字列に変換することができます。この文字列こそが、Edgebreakerが出力する圧縮データになります。

また、この文字列に対し、さらなる圧縮技術を用いることで、1記号あたり平均1ビット未満で保存可能なため、三角形ひとつあたり1ビット以下までの圧縮を可能にしています。従来の保存方式では、三角形一つに対してその頂点のインデックスを、例えば32ビットずつで保存した場合、合計でひと三角形あたり96ビットかかります。しかし、Edgebreakerでは接続性を約100分の1にまで圧縮できることがわかります。

Edgebreakerによる圧縮

それでは、Edgebreakerアルゴリスムの詳細に入っていきましょう。メッシュが位相的に球面と同じであると仮定します。この仮定により、以下のことが保証されます：

1. メッシュが向き付け可能である、つまり、メッシュ全体で一貫した左右の概念を決定できること。例えば、リボンの端と端を一度ひねってからくっつけたようなメッシュは向き付け可能ではありません。実際に、リボン状で左右を決定し、そのままリボンを一周してくると、出発地点の裏側に到達し、左右が逆転してしまいます。
2. 境界が存在しないこと、つまり、各辺がちょうど2つの隣接面を持つこと。
3. メッシュが単連結であること、つまり、メッシュ上のどのループもメッシュ上を通って1点に縮小できること。（例えば、ドーナツの表面のようなメッシュを考えてみましょう。表面上に1点に縮小できないループをいくつか描くことができるはずです！残念ながら、この記事で説明している簡略版のEdgebreakerはこのようなメッシュにも対応していません。）

この条件はもしかすると少し厳しすぎると思われるかもしれません。実際には、これらの条件は取り除くことができ、あらゆる種類のメッシュに対応するようにアルゴリズムを拡張することは可能です。しかし、議論が複雑になることを避けるため、それらのアルゴリズムは本稿では解説せず、次回以降の記事で書いていこうと思います。

このアルゴリスムを走らせる前に、いくつかの下準備が必要です。

まず、すべての頂点と面を「未訪問」に設定します。

また、メッシュ上で左右の概念を決定します。この選択は完全に任意ですが、アルゴリズムの全過程を通じて一貫性を保つ必要があります（上記の条件１によって、そのような選択が可能となります）。

また、メッシュの任意の三角形を最初の「現在の三角形」として選びます。同様に、現在の三角形の任意の辺を最初の「現在の辺」として選びます。「現在の頂点」とは、現在の辺に含まれない三角形の頂点を指します。

ここまでの準備の後、ようやくEdgebreakerを走らせることができます。Edgebreakerの再帰的な定義を以下のように述べることができます：

1. 現在の三角形の面を「訪問済み」としてマークします。同様に、現在の三角形の3つの頂点すべてを「訪問済み」としてマークします。
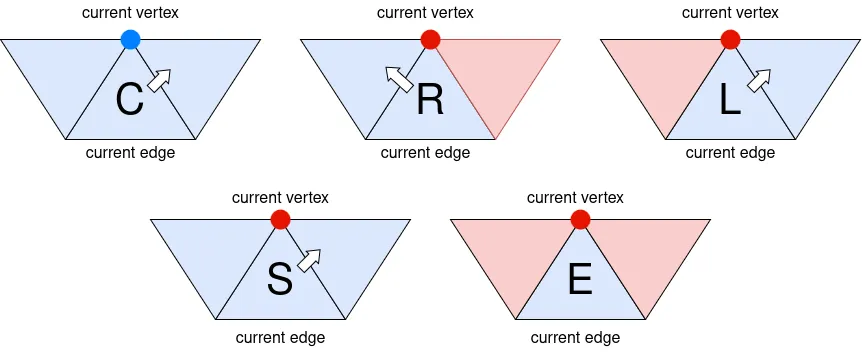
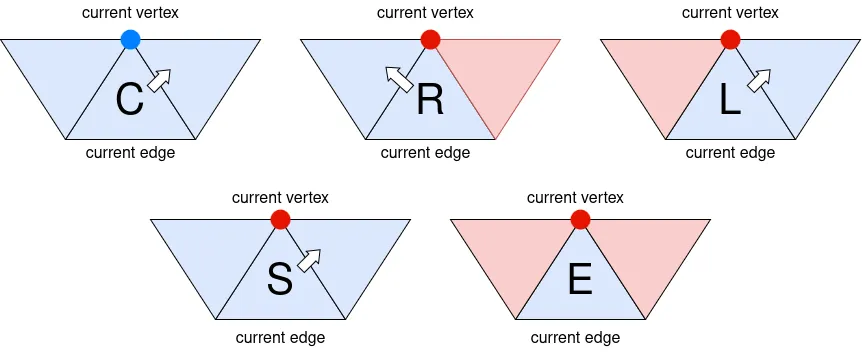
2. 現在の頂点と現在の三角形周辺の面の訪問済みか未訪問かの状態に基づいて、以下のいずれかの記号を出力し、次の反復で現在の三角形となる「次の三角形」を決定します（下図参照）：

   • C (Continue)：現在の頂点が未訪問の場合。この場合、隣接面はすべて未訪問であることが自動的に保証されるため、右の三角形を次の三角形として選びます。

   • R (Right)：現在の三角形の右隣のみが訪問済みの場合。左の三角形を次の三角形として選びます。

   • L (Left)：現在の三角形の左隣のみが訪問済みの場合。右の三角形を次の三角形として選びます。

   • E (End)：現在の三角形のすべての隣接面が訪問済みの場合。最新の「S」と記録されている三角形のうち、左隣が未訪問のものがある場合は、その左隣を次の三角形として設定します。そのような三角形がない場合は、アルゴリズムを終了します。

   • S (Split)：左右の隣接面が共に未訪問だが、現在の頂点が訪問済みの場合。右の三角形を次の三角形として選びます。

3. 「現在の辺」を、「次の三角形」と「現在の三角形」が共有する辺に設定します。また、「次の三角形」の頂点であって「現在の辺」の頂点でないものを「現在の頂点」に設定します。最後に「次の三角形」を「現在の三角形」として設定します。ステップ1に戻ります。

上記の条件の下で、Edgebreakerアルゴリズムは、メッシュ内のすべての三角形を一度だけ確実に訪問することが保証されます。これは以下の理由によります：

1. 各三角形は最大一度だけ訪問されるため（三角形を「訪問済み」としてマークするため）。
2. アルゴリズムは最終的にすべての三角形を訪問されるため（球面位相の仮定により、孤立したコンポーネントが存在しないため）。

時間計算量に関して、このアルゴリズムは非常に効率的です。

• 時間計算量： $O(n),$ ここで$n$はメッシュ内の三角形の数です。各三角形が一度だけ処理され、再帰的な各ステップで定数時間の操作のみが必要であるため、線形時間計算量が達成されます。
• 空間計算量： $O(n)$ これは訪問済みの面と頂点、および出力されたCLERS文字列の保存に必要です。

アルゴリズム中で使われた5つの記号はCLERS記号と呼ばれています。実際にはCLERS文字列の中で半分以上がCであることが知られています。つまり、記号のビット表現を

• C：0
• L：110
• E：111
• R：101
• S：100

と決めることによって平均して2ビット以下での保存が可能になります。圧縮率を更に高めたい場合は、rANS(Ranged Asymmetric Numerical Systems)等のエントロピー符号化アルゴリズムを活用したり、接続性の予測アルゴリズムを活用することで、各三角形あたり1ビット以下で保存することもできます。（Isenburg, M., & Snoeyink, J., 2000）

この効率性とアルゴリズムのシンプルさにより、Edgebreakerは高速な圧縮が必要な実用的なアプリケーションにおいて特に魅力的です。ただし、上記の条件を満たさないメッシュを圧縮する場合は計算量が増加することに注意が必要です。

Edgebrekerの解凍

Edgebreakerではメッシュを5つのシンボルからなる文字列に圧縮しましたが、この文字列から元のメッシュを復元（＝解凍）するにはどうすればよいでしょうか？実は、解凍アルゴリズムは複数の異なるアルゴリズムが存在します。この節では、Rossignacによる最初の論文で紹介された最もシンプルなものを解説します。

アルゴリズムの詳細に入る前に、注意点が一つあります。メッシュの圧縮と解凍によって頂点インデックスが並び替えられる可能性があることです。例えば、2つの三角形からなるメッシュの接続性

$$[0,1,2], [1,2,3]$$

をEdgebreakerで圧縮して解凍すると、

$$[0,1,3], [0,2,3].$$

として解凍されることがあります。これら2つのメッシュは位相的には同値ですが、圧縮データのみからからこの並び替えを一意に計算する方法がないため、頂点インデックスの情報は本質的に失われてしまいます。したがって、頂点インデックスに何らかの値が関連付けられている場合（実際に頂点インデックスには位置や法線といった情報が関連付けられていることがほとんどです）、圧縮時にインデックスの並び替えの情報をなにかしらのかたちで別途保存しておく必要があります。

さて、それでは解凍アルゴリズムを見ていきます。

解凍アルゴリズムは、Edgebreakerが出力した文字列を最初から順番に処理することで動作します。まず、オフセットテーブルと呼ばれるものを事前に計算する必要があります。これはCLERS文字列内の「S」の数と同じサイズの整数の配列で、各「S」シンボルの最初の分岐をなす部分文字列から、以下の計算方法に従って計算します。

• C：-1
• R：+1
• L：+1
• E：+3
• S：-1

例えば、とある「S」に対して「SRCRSEE」という部分配列が与えられている場合は、

$$\text{offset} = -1+1-1+1-1+3+3=5$$

というふうにオフセットを計算します。

また、先ほどと同様に左右の概念を決定し、最初の三角形を作成して、その任意の一辺を最初の「現在の辺」として選択します。また、作成した三角形のすべての辺を「現在の境界」と呼ぶことにします。

次に、文字列内の各シンボルに対して（左から右に）、以下の操作を実行します：

• C (Continue)：新しい頂点を作成し、現在の辺と接続して新しい三角形を形成します。現在の辺を現在の境界から取り除き、新しく作成した三角形の現在の辺以外の２辺を現在の境界に加えます。現在の辺を現在の辺の右頂点と新しい頂点を結ぶ辺に更新します。

• R (Right)：現在の境界上で、現在の辺の右頂点とつながっていて、かつ現在の辺の左頂点ではない頂点を求めます。その頂点と現在の辺で新しい三角形を作成します。現在の辺を、現在の辺の左頂点と新しい頂点を結ぶ辺に更新します。新しい三角形の辺のうち、現在の辺でないものを現在の境界から取り除きます。

• L (Left)：現在の境界上で、現在の辺の左頂点とつながっていて、かつ現在の辺の右頂点ではない頂点を求めます。その頂点と現在の辺で新しい三角形を作成します。現在の辺を、現在の辺の右頂点と新しい頂点を結ぶ辺に更新します。新しい三角形の辺のうち、現在の辺でないものを現在の境界から取り除きます。

• E (End)：これは「S」分岐の終わりを示します。現在の辺の両方の頂点と辺でつながっている頂点が存在するので、その点と現在の辺で新しい三角形を作成します。その後、左隣が訪問されていない最新の「S」の位置に戻り、現在の辺を「S」の左側の辺に更新します。また、新しい三角形のすべての辺を現在の境界から取り除きます。もし、そのような「S」が存在しない場合、アルゴリズムを終了します。

• S (Split)：オフセットテーブルを参照して対応するオフセットを求め、現在の辺の右頂点から、現在の境界を右にオフセット分だけずれたところにある頂点を求めます。この頂点と現在の辺で新しい三角形を作成します。その後、新しい三角形の辺のうち、現在の辺でないものを現在の境界に加え、現在の辺を現在の境界から取り除きます。さらに、現在の辺を、新しい三角形の右側の辺に更新します。

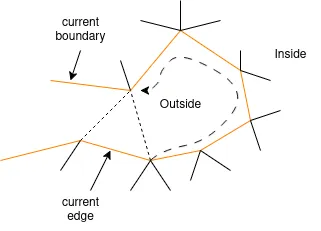
重要なポイントは、各文字が頂点と辺の特定の局所構成に対応しており、これらのルールに従うことで、元々圧縮されたメッシュと同相のメッシュを再構築できるということです。

この解凍アルゴリズムの最悪の場合の計算量は$O(n^2)$で、これはオフセットテーブルを計算する際のコストによるものです。「S」の文字を解凍する際、「S」の最初の分岐を一度先に展開してそこに含まれる文字を処理する必要があるためです。

では、この計算量の上限をさらに下げることは可能でしょうか？

実は、可能です。この章の冒頭で述べたように、Edgebreakerで圧縮されたメッシュを解凍する方法は複数存在し、その中には$O(n)$の時間しか必要としないものもあります。これらの解凍アルゴリズムのバリエーションについては、このシリーズの後半で解説する予定です。

最後に

この記事では一部の簡素なメッシュに対してEdgebreakerの解説をしました。

Edgebreakerアルゴリズムはメッシュの接続性を圧縮できる強力なアルゴリズムです。EdgebreakerのアルゴリスムはGoogleのdracoや、Eukaryaのdraco-oxideで最適な実装がされているので、気になる方はぜひチェックしてみてください。

参照

• Rossignac, Jarek. "Edgebreaker: Connectivity compression for triangle meshes." IEEE transactions on visualization and computer graphics 5.1 (1999): 47-61.
• Duda, Jarek. "Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding." arXiv preprint arXiv:1311.2540 (2013).
• Isenburg, M., & Snoeyink, J. (2000). "Optimized Edgebreaker Encoding for Large and Regular Triangle Meshes." In Data Compression Conference, 2000. Proceedings. DCC 2000 (pp. 520-520). IEEE.