3Dモデルを圧縮する技術2:rANSとは
2025-11-21
こんにちは、Eukaryaの矢所です。
今回は3Dモデル圧縮技術に関する連載記事の第2回として、rANSについて取り上げます。
ranged Asymmetric Numerical System
、略してrANSは、エントロピー符号化と呼ばれる文字の確率分布を利用して文字列を圧縮する圧縮アルゴリズムの一種です。
他のエントロピー符号化と比較して、rANSはその速さと圧縮率の高さで知られています。具体的には、ハフマン符号化と同等の速度を実現しつつ、与えられた確率分布に対して最大の圧縮率を達成できることが保証されています。
rANSはポーランドの計算機科学者J. Dudaによって、Asymmetric Numerical Systems(ANS)と呼ばれる新しいエントロピー符号化族に関する一連の論文の一部として2013年に発表されました。rANSは、その計算効率のよさと数学的に保証された最適性から、またたく間に世界で最も広く使用される圧縮アルゴリズムの一つとなりました。
実際にrANSが使われている例としては、例えば以下のようなものがあります。
- Draco(Googleによる3Dモデルコーデック)
- JPEG XL、AV1(画像/動画コーデック)
- Opus(音声コーデック)
- ZstdおよびLZFSE(MetaおよびAppleによる汎用圧縮アルゴリズム)
また、いくつかのオペレーティングシステムやブラウザなどの基盤システムにも組み込まれていることでも知られており、その普及範囲はもはや計り知れません。まさに今、この記事を表示しているデバイス上でもrANSが動作しているかもしれないーーと言っても過言ではないほど、実はrANSはとても身近なアルゴリズムなのです。
rANSは「3Dモデル圧縮専用技術」というわけではなく、より汎用的な圧縮技術ですが、今回3Dモデル圧縮アルゴリズムの連載にこれを含めているのは、3D圧縮アルゴリズムがrANSコーデックを頻繁に活用しているからです。
例えば、連載の第1回では、メッシュの接続性を特殊な文字列に変換するアルゴリズムであるEdgebreakerアルゴリズムを見てきました。rANSは文字列を圧縮できるため、得られた文字列をrANSコーダーに入力することで、より高い圧縮率を実現できます。さらに、rANSは頂点座標圧縮やテクスチャ座標圧縮に至るまで、幅広く活用されています。
本記事では、rANSアルゴリズムの基礎を解説していきます。
💡 Eukaryaでは、GoogleのDraco 3Dモデル圧縮ライブラリをRustで書き直したdraco-oxideを開発しています。もし興味があればぜひチェックしてみてください!
rANSアルゴリズム
設定と記法
まず、有限な文字の集合を考えて、上に<で示される順序を固定します(例えば、が英語の小文字アルファベットであればa<b<…<zなど)。さらにこれらのアルファベットの確率分布が与えられているとしましょう。確率分布ですので、を満たします。
しかし、rANSが動作するは整数上ですので、固定された正の整数
に対して、離散確率分布と呼ばれる関数
を次の2つの条件を満たすものとして定義します。- 。
- 各について。
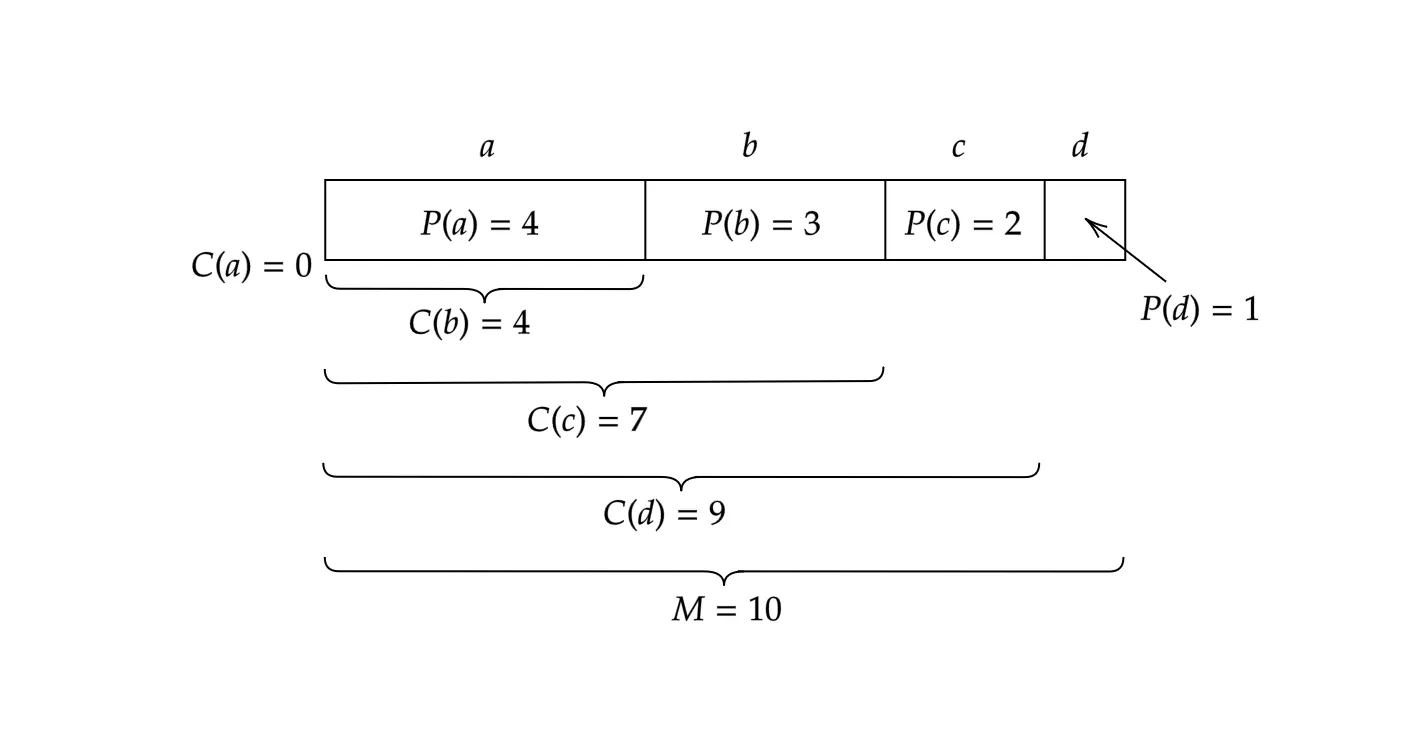
さらに、と定義します。をの範囲へのオフセットと呼ぶことにしましょう。これらの設定は、からまでの整数を個の範囲へと分けるという目的があります。
イメージで理解したい方には、図1が参考になると思います。
圧縮
それでは、実際に圧縮の方法について見ていきます。中の文字でできた文字列(は整数)を符号化したいとしましょう。まず、初期状態をと置きます。rANSはこの状態を再帰的に更新することでと順に計算していき、最終的にを計算します。そのこそがrANSの出力、つまり圧縮データになります。
各再帰ステップの動作は次の通りです。符号化ステップを表す関数をとすると、符号化ステップは各時刻についてと書くことができます(この記事の中では、が固定されている場合、便宜上と書くこともあります)。
まず、をでユークリッド除算した商と余りを計算します。つまり、次を満たす正の整数とを求めます。
次にを以下の式で計算します。
圧縮のステップは以上です。とても単純ですが、何が起こっているかはわかりにくいので、少し解説をします。
値は前の状態の圧縮版を表しています。にをかけているのは、その後に足される数のためにスペースを作るためです。
このことは整数を進法で表現するとわかりやすいです。進法の数にを掛けると各桁が1つずつ左にずれて、最下位の位置に0が挿入されるのがわかると思いますが、こうしてできた数に集合の中からひとつ数を選んで足したところで、2桁目以上の数は変わりません。最後に足されているは0以上以下なので、この条件を満たしているというわけです。
さて、次のですが、これはどの範囲を使っているのかを覚えておくために記録されています。どの範囲を使っているかがわかれば、どの文字が符号化されたかも後で思い出すことができますね。は(1)の式で使われている通り、解凍時にからを復元するために欠かせない情報ですので、記録されています。
解凍
さて、圧縮によって文字列から1つの巨大な整数を作ることに成功しました。しかし、この巨大な整数から一体どのようにして文字列を解凍することができるのでしょうか?この節では解凍の方法を見ていきます。
rANSで符号化されたデータの復号化は、符号化プロセスを逆にたどっていくことによって実現します。これはつまり、最後に符号化された文字が最初に復号化されるということです。
さらに具体的に言えば、個の文字を符号化した後の状態値が与えられているとき、まずを復元し、次にを計算する、というのが各復号化ステップの概要になります。
ここでも必要な記法を導入します。符号化の場合と同様に、復号化関数をで表します。すなわち、各時刻についてと書くことができます。
まずをでユークリッド除算を行います。つまり、次を満たす正の整数とを計算すします。
はより小さい正の整数であるため、を含む範囲を持つ文字が存在することがいえます。すなわち、
という計算をすることでを復元することができます。
ちなみにこの計算は、の各値とそれを含む範囲を持つ文字の表を先に計算しておくことで効率的に実装できます。
が特定できたら、残りはを計算するのみです。まず、次の等式が成り立つことが解ると思います。
ここでとは前の節の符号化関数で定義された値です。等式(3)と(4)を使って等式(1)の変数とを書き換えると、最終的な復号化の式が得られますね。
以上が復号化の1ステップです。復号化のプロセスは、最終的にに到達するまで、繰り返し続けられます。そのたびにを記録し、最終的に得られる文字列が完全に復号化された文字列になります。
ここで、復号化は符号化とは逆の順序で進むことに注意が必要です。つまり、をこの順序で符号化した場合、シンボルはの順序で復号化されるということです。
例
では、簡単な例題を見ていきましょう。
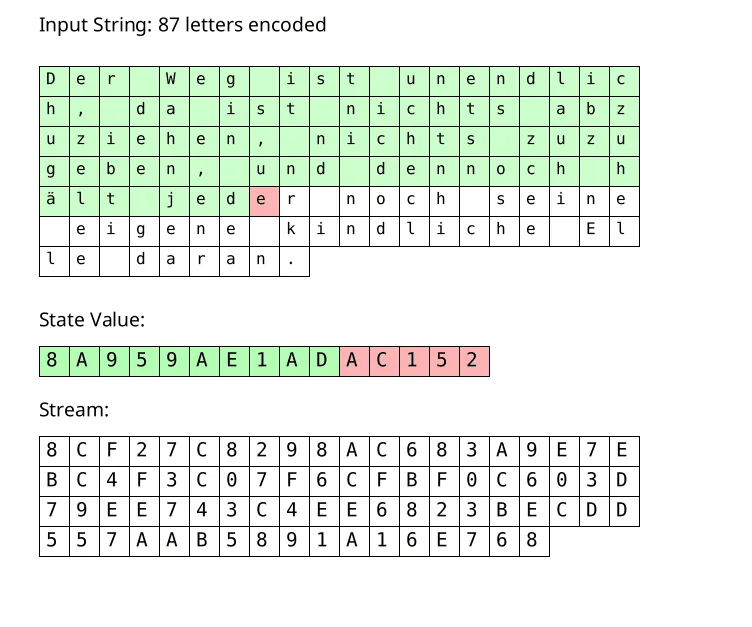
ここでは、図1の設定をそのまま用います。現在までにまで符号化されているとして、ここで6番目の文字として「c」を圧縮してみます。
上記の計算に従うと、、、となることがわかると思います。つまり、が得られます。これだけで圧縮は完了です。
では、からと文字「c」をどのように復号化できるでしょうか?
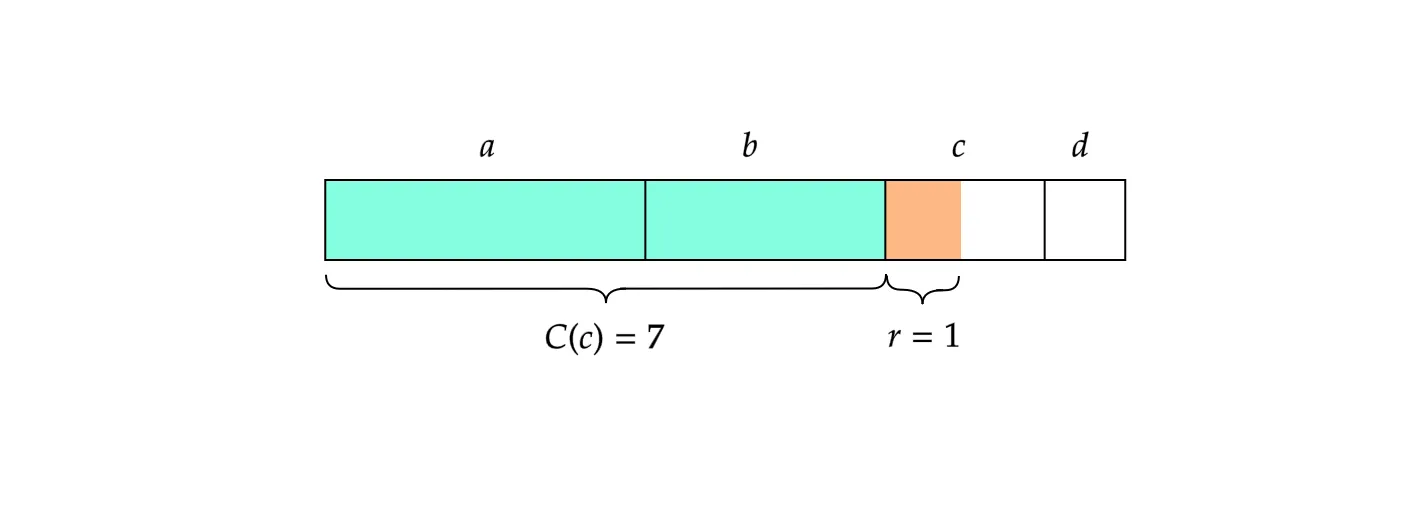
をで割ると商と余りを得ます。から文字と余りを復号化するには、図2を参照してください。(具体的には)であるため、は文字「」の範囲内にあるので、ここで「」を復号化できます。
また、は「c」の範囲内で値を持つことがわかる(図のオレンジの部分)ので、であることがわかりますね。したがって、が得られるというわけです。
ストリーミングrANSアルゴリズム
前の節では、文字列に関するすべての情報を含む巨大な整数を作成することを主なアイデアとするrANSコーデックを紹介しました。
rANSは与えられた確率分布に対して最適なエントロピー符号化を実現することで知られていますが、文字列のサイズが大きくなるにつれて急速に実用的でなくなってしまいます。
というのも、ますます大きくなる整数に対してユークリッド除算を実行する必要があり、ユークリッド除算は整数が何百桁、何千桁と大きくなれば計算がほぼ不可能になってしまうのです。
この問題を解決策として、各状態の値を分解して、適度に小さく保つということが考えられます。これは、ストリーミングrANSとよばれる、rANSに少し変更を加えたアルゴリズムによって実現することができます。
この節ではストリーミングrANSについて解説していきます。
ストリーミング符号化
まず、正の整数とを選択します。この選択は完全に自由ですが、選択するにあたってはいくつかの指標があります。
まずは、ストリームに送信する各転送のビット数を示しています。最も単純な実装ではに設定し、バイトストリームの場合はに設定するのが良いでしょう。
はをどれだけ小さく保つかを示すアルゴリズムのパラメータであり、の値が高いほどアルゴリズムは遅くなりますが、圧縮効率は向上します。
ここで解説するストリームrANSは、各ステップにおいて状態の値がとの間にあることを保証してくれるアルゴリズムです。つまり、
と定義した場合、常にとなることを保証してくれます。例えば、64-bitの非負整数を用いる場合、がを超えないようにrANSを設計することは実装においてひとつの重要なポイントであると言えます。
ストリーミングrANSの考え方自体は非常に単純で、各ステップにおいて、が範囲から外れそうになるときは状態をで割り、余りの数をストリームに出力してしまうことで、を常にの内部に保っています。
さて、状態の値がの範囲から外れようとしていることをそもそもどのようにして知ることができるのでしょうか?言い換えれば、どの状態値と文字のときとなるのでしょうか?この問に答えるには、次のように定義される集合
について詳しく知る必要があります。
この集合を計算するのに役立つ事実として、関数が単調増加であることがあげられます。つまり、入力が大きくなればなるほど、出力も大きくなるという性質を持っているのです(これは簡単に確かめることができます)。
この事実さえあれば、およびの2つの数さえわかればもう上記の問は解決します。なぜなら、単調性により、を持つ任意の数もに含まれることがわかるからです。
では、との実際の値は何でしょうか?もしお時間があれば、とてもいい演習になると思いますので、ぜひご自身で計算してみてください!
… どうでしたでしょうか?それでは答え合わせをしていきます。結果は以下のようになります。
に対するこのすっきりとした式になるのは、実ははそのように設計されているおかげなのです!
したがって、を符号化しようとするときに状態値が上記のの内部にあれば、結果として得られる状態値は決してオーバーフローしないことがわかりましたね。
これでいよいよアルゴリズムを説明する準備が整いました。状態が与えられたとき、シンボルは次のように符号化することができます。
残る疑問はただ一つです。whileループが有限のステップで終了することをどのように担保できるのでしょうか?による除算がを飛び越えてしまう場合は無限ループになってしまいますが、その心配はないのでしょうか?
実は、による除算は区間を飛び越ることは決してありません。これも、の設計のおかげです。もし区間を飛び越える状態値が存在するとするならば、を満たす整数が存在しなければならなくなります。これはまたはを意味しますが、どちらの場合も決して起こり得ないというのは自明なことですよね。これは矛盾となりますから、区間を飛び越えるかもしれないという前述の心配は杞憂であったというわけです。
ストリーミング復号化
普通のrANS同様、復号化は符号化の逆の操作によって行われます。各時刻において、前の節で説明した普通のrANS復号化プロセスを使用して、から文字とを復号化することから始めます。
文字を復号化した後、状態がの下限を下回る場合、符号化されたビットストリームから追加のビットを読み込んでに加え、それを新たにとします。つまり、以下のようにアルゴリズムを定義できます。
しかしここでも、符号化中に行われるビットの読み取りの回数が復号化中の回数と異なり、復号化が失敗するのことがあるのではないかと疑問に思うかもしれません。
特に、となったらビットの読み取りを停止しますが、これは早すぎるということは起きないのでしょうか?もしかしたら、でもある可能性はないでしょうか?
実は、これもの設計により、との両方がに含まれるような整数は存在しないことが保証されています(この事実は上記同様簡単に確かめられるので、演習にご活用ください!)。
これにより、ストリームの読み取り回数が一意に決定されることが保証され、アルゴリズムは前述のような曖昧な状況には遭遇しないのです。
以上です!これで実用的なrANSアルゴリズムが完成しました。
tANSアルゴリズムの概要
最後に、非常に短くではありますが、tANSというrANSと非常に関係の深いアルゴリスムを紹介します。
前の節では、各時刻において状態値を特定の範囲に制限するrANSのストリーミング版を見てきました。は一対一の写像(単射)であるため、rANS符号化プロセス全体を通してに供給される入力は有限個しかありません。
より具体的には、ストリーミングrANSでは、とに対してを定義すれば十分であり、このようなペアは有限個しかないということです。
tANSアルゴリズム(tabled Asymmetric Numerical System)は、符号化/復号化プロセスの開始時にの表を作成することでrANSの速度を向上させる、ANS族の一種です。この表により、ユークリッド除算や整数乗算を含むの計算を、ただの表の参照にまで削減できます。
このアルゴリズムの課題は表の作成方法にあります。のすべての値を計算することもできますが、これではの計算を避けることを目的とするtANSの意義が失われてしまいます。
Jarek Dudaの論文[1]は、これらの表の値を明示的に計算することなくの表を作成する方法を示していますが、その方法を詳しく説明していたら本記事の範囲を大きく超えてしまいますので、今回はこのあたりで御免を蒙ります。
結論
本記事では、あらゆる圧縮の場面において強力なツールとして使われているrANSとそのストリーミング版について紹介いたしました。
基本的なrANSコーダーは文字の出現確率に基づく最適なエントロピー符号化を実現しますが、そのままでは状態値のサイズが増大することによる実用上の制限に直面します。この問題は、多少の圧縮率とのトレードオフはあるものの、ストリーミングrANSという状態値を制限する仕組みを導入することで完全な解決を見ました。
また、圧縮率と計算複雑性の間で異なるトレードオフを提供するANS族の一種であるtANSについても簡単に触れました。
これらの近代エントロピー符号化技術は、3Dモデル圧縮のみならず、さまざまな場面で現代のIT技術を影から支えている、まさに縁の下の力持ちと言ってよいと思います。本稿が、少しでも多くの方にとって、普段陽の当たらない彼らを知るきっかけになれば幸いです。
では、今回はこれにて。
参照
- Duda, J. (2013). Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding. arXiv preprint arXiv:1311.2540. https://arxiv.org/pdf/1311.2540
Eukaryaでは様々な職種で採用を行っています!OSSにコントリビュートしていただける皆様からの応募をお待ちしております!
Eukarya is hiring for various positions! We are looking forward to your application from everyone who can contribute to OSS!
Eukaryaは、Re:Earthと呼ばれるWebGISのSaaSの開発運営・研究開発を行っています。Web上で3Dを含むGIS(地図アプリの公開、データ管理、データ変換等)に関するあらゆる業務を完結できることを目指しています。ソースコードはほとんどOSSとしてGitHubで公開されています。
➔ Re:Earth / ➔ Eukarya / ➔ note / ➔ GitHub
Eukarya is developing and operating a WebGIS SaaS called Re:Earth. We aim to complete all GIS-related tasks including 3D (such as publishing map applications, data management, and data conversion) on the web. Most of the source code is published on GitHub as OSS.