Hi, I am Yadokoro from Eukarya.

At Eukarya, we are developing draco-oxide, a rewrite of the Google’s draco library in the Rust programming language. And I recently released an alpha version on crates.io. It is still under development, but if you are interested in using it, feel free to check out:

https://github.com/reearth/draco-oxide

This article is the first in a series of articles on 3D graphics compression techniques, focusing on the Edgebreaker algorithm.

What is a Mesh?

IIn 3D graphics, a mesh is a data structure composed of a 3D point cloud (i.e., a set of 3D points) and a set of triangles whose vertices are from the point cloud. Meshes are the fundamental data structure for 3D graphics and are used to display virtually any shape in computer graphics.

What is the Edgebreaker Algorithm?

Edgebreaker is a lossless mesh connectivity compression algorithm widely used in 3D graphics, and is used to compress the connectivity part (i.e. the set of triangles) of the mesh. When combined with other compression techniques, it can compress mesh connectivity data to less than 1% of its original size. Thanks to this impressive compression ratio and its simplicity, Edgebreaker has become a de facto standard for mesh compression and is implemented in major libraries such as Google's Draco.

The algorithm was first introduced by Rossignac (1999) for mesh surfaces that are either a disc or a sphere, and later got extended to other orientable manifolds, possibly with multiple boundaries. The idea of the algorithm is very simple: It traverses each triangle by recursively visiting the neighboring triangles, recording the local information about the connectivity as one of predetermined set of symbols. As a result, the connectivity data is converted into a string of symbols, and with some additional techniques such as prediction coding and entropy coding, the mesh connectivity can be compressed to less than a bit per triangle on average.

Compression

Now let’s dive into the the details of the algorithm. We assume that the mesh is topologically the same as a sphere. By assuming this, we can guarantee that:

1. The mesh be orientalble, i.e. we can determine the notion of left and right (or clockwise and counter-clockwise) that is consistent throughout the entire mesh, that
2. There is not a boundary, i.e. each edge has exactly two neighboring faces, and that
3. The mesh has no handles, i.e., any loop on a mesh can be shrunk to a point. (Not all surfaces satisfy this condition. Think of the surface a donut; you can draw loops on it that cannot be shrunk to a point! Unfortunately, the Edgebreaker algorithm as explained in this article does not work for these surfaces.)

You may think that this condition is a bit too restrictive. And yes, it is certainly possible to relax the condition and extend the algorithm to all kinds of meshes. However, it is out of the scope for this article.

We start by setting all the vertices and faces as “unvisited”. We also need to determine the notion of “left and right”, or, equivalently, “clockwise or counter-clockwise” on the mesh. Even though this choice is arbitrary, we need to be consistent during the entire process of the algorithm. (And this is the reason why required the orientability above!)

Furthermore, we choose an arbitrary triangle of a mesh as our first current triangle. Similarly, choose an arbitrary edge of the current triangle to be our first current edge. By the current vertex, we mean the corner vertex of the current triangle that is not the contained in the current edge. Now we can finally state the recursive definition of the Edgebreaker as follows:

1. Mark the face of the current triangle as "visited". Similarly, mark all of the three corner vertices of the current triangle as “visited”.
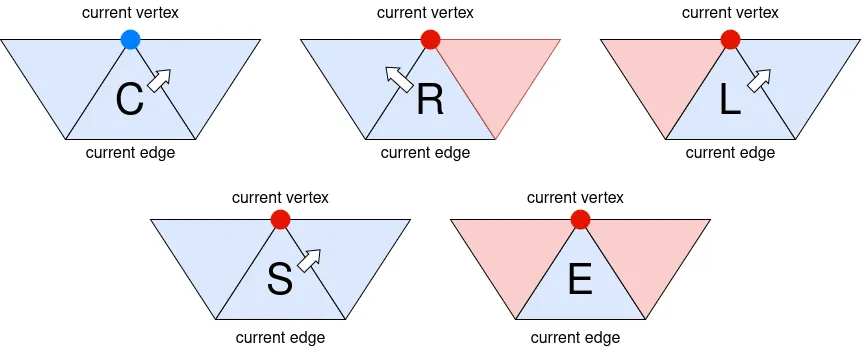
2. Based on the visited conditions of the current vertex and the faces around the current triangle, output one of the following symbols, and determine the next triangle, which will be our current triangle in the next iteration (refer to the figure below):
   • C (Continue): The current vertex is unvisited. Then it is automatic that none of the neighboring faces are unvisited. Choose the right triangle as the next triangle.
   • R (Right): Only the right neighbor of the current triangle is visited. Choose the left triangle as the next triangle.
   • L (Left): Only the left neighbor of the current triangle is visited. Choose the right triangle as the next triangle.
   • E (End): All neighbors of the current triangle are visited. Set the next triangle to be the left neighbor of the most recent “S” triangle whose left neighbor is unvisited, if there is any. If there is not such triangle, we terminate the algorithm.
   • S (Split): Both left and right neighbors are unvisited, but the current vertex is visited. Choose the right triangle as the next triangle.
3. Set the next triangle as the current triangle, and set the the current edge and the current vertex. Go back to step 1.

Regarding time complexity, the algorithm is highly efficient:

• Time Complexity: $O(n),$ where $n$ is the number of triangles in the mesh. The linear time complexity is achieved because each triangle is processed exactly once (as we mark the triangle as “visited”) and because only the constant time operation is necessary at each of the recursive step.
• Space Complexity: $O(n)$ for storing the visited faces and vertices and the output symbol string.

This efficiency, combined with the algorithm's simplicity, makes Edgebreaker particularly attractive for real-world applications where fast compression is required.

Finally, we discuss about the compression rate. The five symbols used in the algorithm are called CLERS symbols. It is known that more than half of the CLERS string consists of C symbols. Therefore, by defining the bit representation of symbols as:

• C: 0
• L: 110
• E: 111
• R: 101
• S: 100

storage is possible with less than 2 bits on average. If even higher compression ratio is desired, one can use the entropy coding algorithms such as rANS (Ranged Asymmetric Numerical Systems, [Duda, Jarek, 2013] ) or the prediction scheme introduces by Isenburg, et al (2000), which allow us to store the mesh to less than a bit per triangle.

Decompression

Now we have compressed the mesh into a string of five symbols, how can we revert the compression to get the original mesh from the string? It turns out that there are multiple different algorithms to achieve the same goal, and in this article we will explain the simplest one appeared in the very original paper by Rossignac.

Before diving into the algorithm, we need to note that the encoding and decoding a mesh can get the vertex indices permuted. This means that, for example, a two-triangle mesh

$$[0,1,2], [1,2,3]$$

encoded and decoded by the Edgebreaker can be decoded as

$$[0,1,3], [0,2,3].$$

These two meshes are topologically equivalent, but we essentially lost the information of the vertex indices as there is no canonical way of computing this permutation from the CLERS symbols. Hence, the indices information must be saved elsewhere during the encoding if any values are associated with vertex indices (which is most likely the case in practice as vertices often have position or normal).

The decompression algorithm works by replaying the Edgebreaker symbols. First, we need to pre-compute what is called the offset table. It is an array of integers of size the number of ‘S’ symbols in the CLERS string, and is computed as follows: For each symbol ‘S’ get the substring starting from it and ends at the ‘E’ symbol that indicates the end of its first branch. Then for each symbol in the substring, look at the following table to get the corresponding summand and take the sum.

• C：-1
• R：+1
• L：+1
• E：+3
• S：-1

For example, if an ’S’ symbol has the substring “SRCRSEE”, then the offset for it will be

$$\text{offset} = -1+1-1+1-1+3+3=5.$$

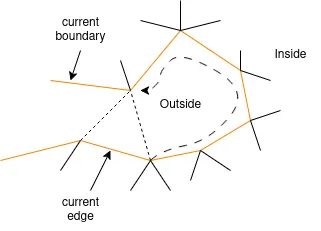
Also, determine the notion of left and right as before, create an initial triangle, and choose some edge as our first current edge. Finally, we call the set of edges of the initial triangle as current boundary.

Now, for each symbol in the string, we perform the following operations:

• C (Continue): Create a vertex and form a new triangle with the vertex and the current edge. Remove the current edge from the current boundary, add to the current boundary the two edges of the new triangle that is not the current edge. Update the current edge to the edge formed by the right vertex of the current edge and the new vertex.
• R (Right): Let the current vertex be the vertex on the active boundary that is right-adjacent to the right vertex of the current edge. Create a new triangle with it and the current edge. Update the current edge to be the edge of the right vertex of the current edge and the current vertex. Add the current edge to the current boundary, and remove the other edges of the new triangle from the current boundary.
• L (Left): Let the current vertex be the vertex on the active boundary that is left-adjacent to the left vertex of the current edge. Create a new triangle with it and the current edge. Update the current edge to be the edge of the left vertex of the current edge and the current vertex. Add the current edge to the current boundary, and remove the other edges of the new triangle from the current boundary.
• E (End): This marks the end of a branch. Create a new triangle with active edge and the unique vertex on the current boundary that is adjacent to both vertices of the active edge. Remove all the edge of the new triangle from the current boundary. Return to the most recent 'S' operation's face whose edge is on the current boundary, and update the current edge to that edge.
• S (Split): Compute the vertex on the current boundary that is $o$ vertices away from the right vertex, where the number $o$ is the offset number for the symbol from the offset table. Create a new triangle with this vertex and the current edge. Remove the current edge from the current boundary, and add the edges of the new triangle that is not the current edge to the current boundary. Update the current edge to the edge formed by the right vertex of the current edge and the vertex computed above.

The worst case complexity of this decoding algorithm is $O(n^2)$, and this is due to the cost of “looking ahead” when computing the offset table. To be precise, when we decode the ‘S’ symbol, we have to expand the first branch and count the number of symbols in it. Could this complexity bound be any lower? The answer is indeed yes, and as mentioned in the beginning of this section, there are multiple different ways to decode the meshes compressed by the Edgebreaker, and some of them are require only $O(n)$ time. We are going to explain the variants of the decoding algorithm later in the series.

Conclusion

The Edgebreaker algorithm is a powerful algorithm that can compress mesh connectivity. In this article, we explained Edgebreaker for some simpler meshes. The Edgebreaker algorithm has been optimally implemented and integrated in Google's Draco library and Eukarya's draco-oxide library, so please check them out if you're interested.

Reference

• Rossignac, Jarek. "Edgebreaker: Connectivity compression for triangle meshes." IEEE transactions on visualization and computer graphics 5.1 (1999): 47-61.
• Duda, Jarek. "Asymmetric numeral systems: entropy coding combining speed of Huffman coding with compression rate of arithmetic coding." arXiv preprint arXiv:1311.2540 (2013).
• Isenburg, M., & Snoeyink, J. (2000). "Optimized Edgebreaker Encoding for Large and Regular Triangle Meshes." In Data Compression Conference, 2000. Proceedings. DCC 2000 (pp. 520-520). IEEE.